Pero solo desde un punto de vista numérico.
Hemos ido construyendo distintos conjuntos de números, según las necesidades y las operaciones que queríamos hacer con ellos. Los
números naturales,
{0, 1, 2, 3...}, nos servían para contar y hacer algunas sumas. Pero no podíamos resolver ecuaciones como

, porque no existe ningún número que sumado a
8 de
3, de otra forma, no podemos realizar la operación
3-8, no al menos con números naturales; pero los matemáticos son gente con recursos y se inventaron los números negativos, que junto con los naturales forman el conjunto de los
números enteros. Luego quisimos resolver ecuaciones como
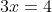
, y entonces los matemáticos nos resolvieron el problema inventando las fracciones, que junto con los enteros forman el conjunto de los
números racionales, y después nos empeñamos en seguir resolviendo ecuaciones y en complicarnos la vida y nos empeñamos en que la ecuación
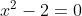
tenía que tener solución. Entonces los matemáticos inventaron los
números irracionales, para disgusto de Pitágoras, y ya tenemos todos los
números reales.
Estos últimos, los irracionales, se pueden clasificar en números algebraicos y números trascendentes. Los números algebraicos son los números reales que son solución de una ecuación polinómica del tipo de la que tenemos abajo (ésta es de grado 3)
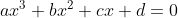
pero con la condición de que los coeficientes
a,
b,
c y
d sean números racionales, es decir números enteros o fracciones. Por ejemplo la solución de la ecuación
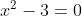
es

, que es un número algebraico. También es algebraico el número de oro, del que hablábamos en la primera entrada del blog. Los números irracionales que no son solución de una ecuación de este tipo son
números trascendentes. Puede parecer que la mayoría de los números irracionales son algebraicos, pero nada más lejos de la realidad. Nos pasamos la vida resolviendo ecuaciones algebraicas, cuando la mayoría de los números son trascendentes.
Quizás el número trascendente más famoso es

, es un número familiar desde la escuela y lo obtenemos cuando dividimos la longitud de la circunferencia entre su diámetro.

es un número divertido que aparece donde menos lo espera uno, en la teoría de probabilidades, en la física... En general los números trascendentes son bastante simpáticos y se puede pasar un buen rato con ellos.
Otro número trascendente famoso es la constante de Euler más conocida como el número
e, que tiene un valor aproximado de
 y
y 
son los números trascendentes más populares y además hay una bonita relación entre ellos y otro curioso número que los matemáticos han inventado para poder seguir resolviendo ecuaciones raras , el
número imaginario 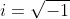
. Esta relación en forma de igualdad,
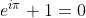
, es una relación natural y trivial para un matemático.
Hay muchos números trascendentes, tantos como infinitos, pero algunos más populares que otros, por ejemplo la constante de Liouville, el número de Catalán... Si haces click
aquí los encuentras.
Vamos a hacer un pequeño ejercicio de matemática financiera (muy de moda en estos días). Si vamos a nuestro banco el 1 de enero con 1€ y conseguimos que el director nos abra un depósito con un interés del 100% a un año, el 1 de enero del año siguiente tendremos 2€. Pero el director del banco es un tipo
enrollao y me propone que al cabo de medio año vaya a recaudar mis intereses y los reinvierta en el depósito. Entonces yo voy el día 1 de julio, recojo mi medio euro de intereses (el 50%) y lo reinvierto, así durante el segundo semestre voy a tener invertido 1,5 euros y el interés que me tienen que dar es el 50% de esto, es decir 0,75€. Total que he hecho un buen negocio porque al final de año tengo 25 céntimos más.
Pero el director va más allá y me dice que por qué no recojo mis intereses cada trimestre. Como hay cuatro trimestres en el año me pueden dar cada vez el 25% de lo que tengo y reinvertirlo durante el trimestre siguiente. Un sencillo cálculo me da como capital final
Esto va bien, así que le propongo al director que por qué no me deja recoger los intereses cada mes, o mejor cada día, y así, aunque sea un poquito de interés, se va acumulando para el siguiente período. Pero ya la avaricia me ha poseído y quiero capitalizar mis intereses (que es como se llama esto en realidad) continuamente, cada segundo si puede ser, o cada medio segundo, o cada centésima de segundo, y yo que me creo muy listo sé que con esto voy a arruinar el banco y me voy a hacer el más rico del mundo, y hago al cuenta y resulta que lo más que voy a conseguir con mi depósito al 100% de interés y recogiendo intereses y reinvirtiendo continuamente es 2,7182818... euros, el máldito número trascendente.




